0059: Cairo III – Circles and Arcs
Let’s jump right in and look at…
Drawing a Circle
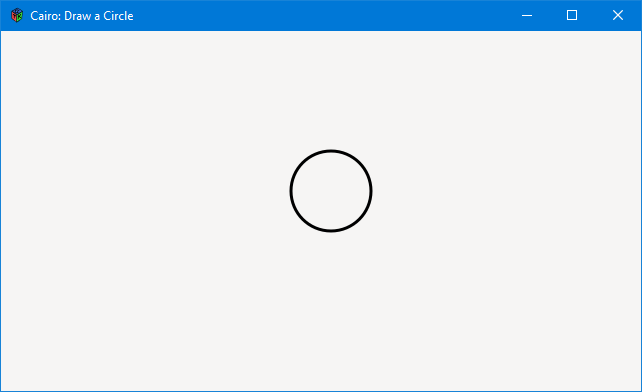
The essence of circle drawing is this:
bool onDraw(Scoped!Context context, Widget w)
{
context.setLineWidth(3);
context.arc(330, 160, 40, 0, 2 * 3.1415);
context.stroke();
return(true);
} // onDraw()
And even though you might expect a circle() function, we actually use arc()… and since an arc is just an incomplete circle, well… there you go.
The arguments to the arc() function are:
- x position of the circle’s center,
- y position of the circle’s center,
- the circle radius (as if the circle were complete),
- the point along the arc where we start drawing, and
- the point along the arc where we stop drawing.
Those last two arguments are in radians. That’s why the point where we stop drawing is two times PI.
The Wikipedia/Cairo Anomaly
When I first started exploring the arc() function, I wasn’t getting the results I expected. My confusion was twofold:
- I had assumed that 0 degrees (and therefore 0.0 radians) was true north like it is on a compass, and
- I also assumed that, like a compass, degrees increase in a clockwise direction around the circle.
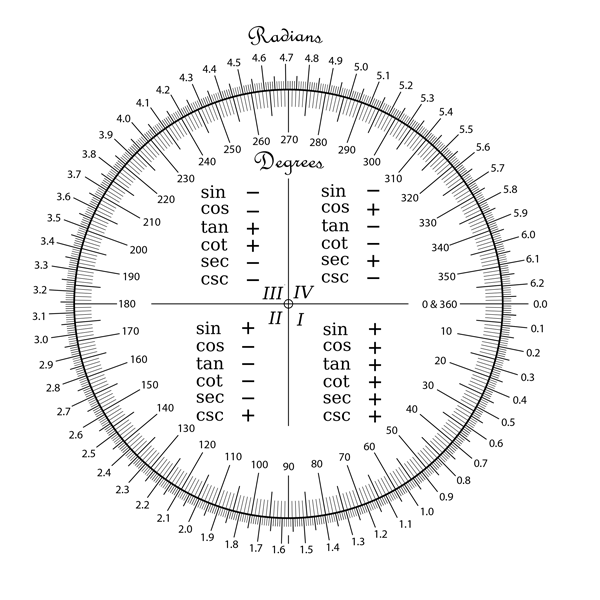
So, I Googled radians and read the Wikipedia page. However, their conversion chart showed 0 to the east, compass-wise, and both degrees and radians increasing counterclockwise.
Eventually, I realized that Cairo agreed with Wikipedia on one count, but not the other.
So, here’s the straight dope on radians according to Cairo:
- 0 is to the east (compass east), and
- radians increase in value in a clockwise direction.
Not being much of a mathematician, I have no idea why 0 faces east and I certainly don’t know why Wikipedia’s conversion chart has radians increasing in a counter-clockwise direction. But Cairo agrees with real-world clocks and compasses, so at least we have those as jumping off points for understanding what’s going on with Cairo arcs.
So I took the liberty of reproducing the conversion chart so it accurately reflects Cairo’s worldview:
Drawing an Arc
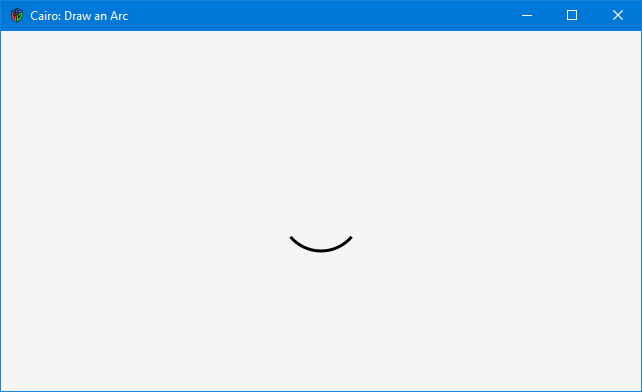
You may be ahead of me on this one, but drawing an arc is the same as drawing a circle except that the start and end points stop short of describing the entire circle:
bool onDraw(Scoped!Context context, Widget w)
{
float x = 320, y = 180;
float radius = 40, startAngle = 0.7, endAngle = 2.44;
// draw the arc
context.setLineWidth(3);
context.arc(x, y, radius, startAngle, endAngle);
context.stroke();
return(true);
} // onDraw()
If you consult the conversion chart, you’ll see that the arc starts at about 40 degrees (south-southeast in Cairo’s version of the universe) and goes to 140 degrees. And remember, drawing is done in a clockwise direction, so even though the start point is to the right of the end point (effectively, right to left) it’s still a clockwise stroke().
Conclusion
Next time, we’ll continue on and cover fills, then double back and have a bit of fun with arcs.
Comments? Questions? Observations?
Did we miss a tidbit of information that would make this post even more informative? Let's talk about it in the comments.
- come on over to the D Language Forum and look for one of the gtkDcoding announcement posts,
- drop by the GtkD Forum,
- follow the link below to email me, or
- go to the gtkDcoding Facebook page.
You can also subscribe via RSS so you won't miss anything. Thank you very much for dropping by.
© Copyright 2025 Ron Tarrant
